Medidas de dispersión
A menudo escuchamos que en los países latinoamericanos existe mucha DIFERENCIA entre los ingresos que perciben por ejemplo los políticos y los trabajadores de otra clase social de la población. Esas diferencias tienen sus raíces en distintos fenómenos sociales, políticos y económicos; sin embargo, un economista diría “el ingreso per cápita en los países latinoamericanos está más DISPERSO que el ingreso per cápita de los países desarrollados”.
El concepto de DISPERSIÓN resulta importante en casi todos los estudios, ya que puede darse el caso de poblaciones con igual valor central (Media aritmética, Mediana o Moda), pero una puede estar más DISPERSA que la otra, es decir, los promedios nos sirven para describir los datos representados por la tendencia central del conjunto. Por lo tanto, el promedio no logra por si mismo describir completamente a una colección de datos; se necesitan otros valores que nos indiquen el grado en que las observaciones estudiadas se apartan o VARÍAN con respecto al valor central, es decir, el GRADO DE VARIACIÓN O DISPERSIÓN.
MEDIDAS DE DISPERSIÓN PARA DATOS NO AGRUPADOS
DESVIACIÓN MEDIA, VARIANZA, DESVIACIÓN ESTANDAR O TÍPICA Y COEFICIENTE DE VARIACIÓN,que son medidas de dispersión que tienen relación con la media aritmética, y por sus propiedades algebraicas son las de más frecuente aplicación y de mayor importancia.
PERO ANTES QUE NADA …
¿QUE ES EL DESVÍO O DESVIACIÓN ?
El desvío de cada observación (o dato) es la DIFERENCIA ENTRE LA OBSERVACIÓN (o el dato) Y LA MEDIA ARITMÉTICA. El desvío es un concepto fundamental que nos permitirá comprender posteriormente otras medidas de dispersión. Por lo tanto.
Desvío ( d ) = x1 – x
Pero hagamos un ejemplo…
Si el conjunto de datos son: 4, 2, 5, 8, 2, 1, 7, 8, 5, y 7 su media aritmética es = 4.9
¿Cuál es la dispersión de cada dato? ¿Cuál es el dato que está mas disperso? ¿Cuál es el dato menos disperso?
Ordenamos los datos de menor a mayor 1, 2, 2, 4, 5, 5, 7, 7, 8, 8 y grafiquemos
1 2 4 4.9 7 8 9
Según la fórmula anterior, desvío es igual al dato menos la media aritmética por lo tanto tenemos:
Datos
|
Calculo del desvío
d = X1 -
|
desvío =
|
1
|
1 – 4.9 =
|
- 3.9
|
2
|
2 – 4.9 =
|
-2.9
|
2
|
2 – 4.9 =
|
-2.9
|
4
|
4 – 4.9 =
|
-0.9
|
5
|
5 – 4.9 =
|
0.1
|
5
|
5 – 4.9 =
|
0.1
|
7
|
7 – 4.9 =
|
2.1
|
7
|
7 – 4.9 =
|
2.1
|
8
|
8 – 4.9 =
|
3.1
|
9
|
8 – 4.9 =
|
3.1
|
49/10=
4.9
|
-10.6
+10.6= 0.0
|
De acuerdo a los resultados de la tabla ¿Cuál es el dato que está más disperso?
Es el número 1, porque independientemente de su signo, su valor absoluto es el mas alto y es de – 3.9 de desvío.
Ahora ¿Cuál es el dato menos disperso?. Es el número 5 porque está más cerca de la media aritmética y tiene un desvío de 0.1.
Si observas la tabla anterior en muy importante obtener primero el valor de la media aritmética que en nuestro caso fue de 49 / 10 = 4.9 para después restarle al valor de cada dato, dicha media.
Por otro lado, al sumar los resultados NEGATIVOS de los desvíos nos arroja un valor de – 10.6 y al sumar los resultados POSITIVOS de los desvíos también nos da un valor de + 10.6 por lo tanto, se comprueba que la diferencia de los desvíos negativos y los positivos, nos da cero o en su defecto tiende a ser cero.
Ahora resolvamos un problema para utilizar las medidas de dispersión
DESVIACIÓN MEDIA, VARIANZA, DESVIACIÓN ESTANDAR O TÍPICA Y COEFICIENTE DE VARIACIÓN
CON D A T O S N O A G R U P A D O S
Número de muestra
|
DATOS de la resistencia del concreto kg/cm2
|
1
2
3
4
5
6
|
358
369
363
358
336
341
|
Un constructor, para asegurarse de la calidad de su obra, tomó seis muestras de concreto y obtuvo los resultados del cuadro.
Al preguntarle uno de sus colaboradores ¿Cuál de todas las muestras del grupo era la más dispersa?
el constructor elaboró la siguiente tabla:
Número de muestra
|
Resistencia
Kg/cm2
|
desvíos
d = x1 –
|
1
2
3
4
5
6
|
358
369
363
358
336
341
|
358 – 354.17 = 3.83
369 – 354.17 = 14.83
363 – 354.17 = 8.83
358 – 354.17 = 3.83
336 – 354.17 = -18.17
341 – 354.17 = - 13.17
|
Suma =2125
| Diferencia = 0.02 | |
2125/6= Media =354.17
|
Finalmente el constructor en base a la tabla y a los cálculos realizados le indicó a su colaborador:
LA MUESTRA NÚMERO 5 ES LA MÁS DISPERSA, DEBIDO A QUE OBTUVO EL MAYOR VALOR ABSOLUTO DE DESVÍO CON -18.17.
En este caso particular, el mayor valor tuvo el signo negativo lo que significa que la observación es menor que el valor de la media.
VIDEO SOBRE LAS MEDIDAS DE DISPERSIÓN PARA DATOS NO AGRUPADOS
Desviación media
La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.
La desviación media se representa por 

Ejemplo
Calcular la desviación media de la distribución:
9, 3, 8, 8, 9, 8, 9, 18
Desviación media para datos agrupados
Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la desviación media es:

Ejemplo
Calcular la desviación media de la distribución:
| xi | fi | xi · fi | |x - x| | |x - x| · fi | |
| [10, 15) | 12.5 | 3 | 37.5 | 9.286 | 27.858 |
|---|---|---|---|---|---|
| [15, 20) | 17.5 | 5 | 87.5 | 4.286 | 21.43 |
| [20, 25) | 22.5 | 7 | 157.5 | 0.714 | 4.998 |
| [25, 30) | 27.5 | 4 | 110 | 5.714 | 22.856 |
| [30, 35) | 32.5 | 2 | 65 | 10.714 | 21.428 |
| 21 | 457.5 | 98.57 |
LA VARIANZA
La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística.
La varianza se representa por  .
.


Varianza para datos agrupados


Para simplificar el cálculo de la varianza vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.

Varianza para datos agrupados

Ejercicios de varianza
Calcular la varianza de la distribución:
9, 3, 8, 8, 9, 8, 9, 18
Calcular la varianza de la distribución de la tabla:
| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60 | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |
Propiedades de la varianza
1 La varianza será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.
2 Si a todos los valores de la variable se les suma un número la varianza no varía.
3 Si todos los valores de la variable se multiplican por un número la varianza queda multiplicada por elcuadrado de dicho número.
4 Si tenemos varias distribuciones con la misma media y conocemos sus respectivas varianzas se puede calcular lavarianza total.
Si todas las muestras tienen el mismo tamaño:
Si las muestras tienen distinto tamaño:
Observaciones sobre la varianza
1 La varianza, al igual que la media, es un índice muy sensible a las puntuaciones extremas.
2 En los casos que no se pueda hallar la media tampoco será posible hallar la varianza.
3 La varianza no viene expresada en las mismas unidades que los datos, ya que las desviaciones están elevadas al cuadrado.
DESVIACIÓN TIPICA O STANDARD
La desviación típica es la raíz cuadrada de la varianza.
Es decir, la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación.
La desviación típica se representa por σ.


Desviación típica para datos agrupados


Para simplificar el cálculo vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.


Desviación típica para datos agrupados


Ejercicios de desviación típica
Calcular la desviación típica de la distribución:
9, 3, 8, 8, 9, 8, 9, 18
Calcular la desviación típica de la distribución de la tabla:
| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60) | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |
Propiedades de la desviación típica
1 La desviación típica será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.
2 Si a todos los valores de la variable se les suma un número la desviación típica no varía.
3 Si todos los valores de la variable se multiplican por un número la desviación típica queda multiplicada por dicho número.
4 Si tenemos varias distribuciones con la misma media y conocemos sus respectivas desviaciones típicas se puede calcular la desviación típica total.
Si todas las muestras tienen el mismo tamaño:


Observaciones sobre la desviación típica
1 La desviación típica, al igual que la media y la varianza, es un índice muy sensible a las puntuaciones extremas.
2 En los casos que no se pueda hallar la media tampoco será posible hallar la desviación típica.
3 Cuanta más pequeña sea la desviación típica mayor será la concentración de datos alrededor de la media.
Interpretación: La dispersión relativa es de un 36%
Significa que la mayor parte de la variabilidad está en torno a una media de 29,4 años ±10,6 años (como aceptamos años cumplidos, consideramos que la desviación típica son 10 años): entre los 19,4 años y los 39,4 años.
Se trata, por tanto, de una distribución muy dispersa.
COEFICIENTE DE DESVIACIÓN DE PEARSON O DISPERSIÓN RELATIVA (CV)
Con este coeficiente podemos conocer el peso de la desviación típica respecto de la media. En otros términos podemos cuantificar la dispersión relativa.
Interpretación: La dispersión relativa es de un 36%
La mayoría de
las ocasiones, no sólo se necesita identificar la relación entre dos variables;
sino que, se necesita
cuantificar el valor
de tal relación.
El método más
usual para medir
la intensidad de la
relación lineal entre
dos variables es
la correlación momento-producto o correlación de Pearson, al cual se
identifica generalmente como r.
El coeficiente
de correlación lineal de Pearson (r)
expresa el grado de relación o efecto que tiene el cambio de una variable sobre
otra. Podemos considerar que es, la medida de la intensidad de la relación
lineal entre dos variables. Es un índice estadístico que permite medir la fuerza
de la relación lineal entre dos variables. Su resultado es un valor que fluctúa entre –1 (correlación perfecta de sentido negativo)
y +1 (correlación perfecta de sentido positivo).
Cuanto más cercanos
al 0 sean
los valores, indican
una mayor debilidad
de la relación
o incluso ausencia de correlación
entre las dos variables.
-1 ≤
r ≤ 1
Es importante
señalar que la existencia de correlación entre variables no implica causalidad
y que si no hay correlación de ningún tipo entre dos variables, tampoco habrá
correlación lineal, por lo que r = 0. Sin embargo, el que ocurra r = 0 sólo nos dice que no hay correlación lineal, pero
puede existir correlación de otro tipo.
La media y la varianza son sólo dos casos especialmente importantes de lo que se conoce comomomentos de una distribución. Los momentos de una distribución describen en general la forma geométrica de una distribución estadística. son medidas obtenidas a partir de todos sus datos y de sus frecuencias absolutas. Estas medidas caracterizan de tal forma a las distribuciones que si los momentos de dos distribuciones son iguales, diremos que las distribuciones son iguales. Podemos decir que dos
distribuciones son más semejantes cuanto mayor sea el número de sus
momentos que coinciden.
distribuciones son más semejantes cuanto mayor sea el número de sus
momentos que coinciden.
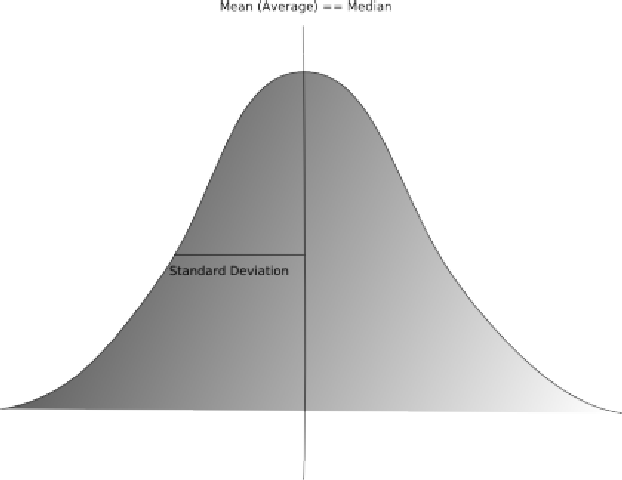
Así, la media sería el primer momento de una distribución estadística y nos daría información sobre dónde se encuentra centrada dicha distribución.
 |
| Pincha en la imagen para verla más grande |
El segundo momento de una distribución estadística, la varianza, nos indica la dispersión de los puntos de dicha distribución, en otros términos, como de ancha es dicha distribución.
Momentos superiores nos informarían sobre la asimetría de una distribución y el grosor de las colas de una distribución... Momentos aún más superiores describen progresivamente detalles geométricos más minuciosos de la distribución.
El conocimiento completo de todos los momentos de una distribución es equivalente al conocimiento de la distribución.
El conocimiento completo de todos los momentos de una distribución es equivalente al conocimiento de la distribución.
 |
| Pincha en la imagen para verla más grande |
EJEMPLO DE "MOMENTO DE UNA DISTRIBUCIÓN"
 |
| Pincha en la imagen para verla más grande |
Significa que la mayor parte de la variabilidad está en torno a una media de 29,4 años ±10,6 años (como aceptamos años cumplidos, consideramos que la desviación típica son 10 años): entre los 19,4 años y los 39,4 años.
Se trata, por tanto, de una distribución muy dispersa.
VIDEO MEDIDAS DE DISPERSIÓN
Fuentes:
Antología de Matemáticas V para el sistema abierto,
DGETA, SEMS SEP
Módulo de aprendizaje de Probabilidad y estadística cecytes
ESTADÍSTICA, Murray R. Spiegel, Larry J. Stephens, Cuarta
edición serie Schaum
Estadística básica con aplicaciones en MS Excel, Juan Carlos
Vergara Schmalbach Víctor Manuel Quesada Ibargüen
Introducción a la probabilidad y estadística 13a.
EDICIÓN, William Mendenhall, Robert J. Beaver, Barbara M. Beaver, Cengage Learning Editores, S.A. de C.V.,











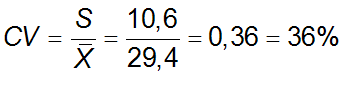
No hay comentarios:
Publicar un comentario